ジュニアスクール３年部授業参観
先日、ジュニアスクール３年部では授業参観が行われました。お忙しい中、お越しいただいた保護者の皆様、誠にありがとうございました。
今回はこの参観授業の算数についてご紹介させていただこうと思います。今回の算数は「見える？見えない？」でした。これは、「今日は、さいころをしっかり見て、さいころの秘密を見つけよう！！」という、さいころづくしの単元なのです。
まずは、全員に実物のさいころを１つずつ渡し、「さいころには面がいくつあるかな？」という基本的なところから始めます。大人にとっては、さいころが「正六面体」であることを当たり前のように理解できますが、まだ辺や頂点の学習をしている最中の子ども達にとっては、一つ一つが大切な学習です。遊びの中で触れる機会の多いさいころですから目の数についてはよく分かっていても、改めて面や辺、頂点の数などを問われると戸惑ってしまう子もチラホラ･･･。
その後、みんなで発表しあいながら、「① 面は６つで、全て正方形」「② 頂点は８つ。辺は１２本で、全て同じ長さ」という２点を確認することができました。その上で、今度は３つ目の秘密を探します。さいころの目を見ながらすぐに発見した子もいましたが、最初はなかなか気が付かなかった子も、先生からヒントをもらうと「向かいあう面の目の数を足すと７になる」という秘密をしっかり見つけ出すことができました。
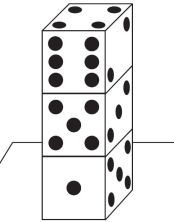
無事に３つの秘密を見つけ出したところで、今度は２つのグループに分かれ、それぞれに３つずつさいころが渡されました。そして、いよいよ今日一番の難問に取り組みます。先生から、「縦に３つ積まれたさいころの面のうち、どの方向からも見えない面の目の数を合計すると、いくつになるでしょう？」という問題が出されました。
この「見えない面」という言葉がクセモノで、自分の位置から「見えない」ことと、さいころ同士や机と重なっていることで「見えない」ことの違いがうまく頭の中で処理できないと混乱してしまいます。事前の授業研究でも、これをどのように分かりやすく説明すればよいかという点は重要ポイントとして考えていました。そのため、問題を解く前に、先生からこの点に関して何度も丁寧に説明され、それを聞いた一方のグループは、言葉の違いをしっかり整理し、見える面の目の数を考えるところから取り組み始めました。･･･が、もう一つのグループでは、同じように見える面の目を考え始めたまではよかったのですが、確認してみると「あれれ、その面見えるかな？」「そこは見えないよね」ということが･･･。
実は、この問題は「向かいあう面を足すと７」というさいころの秘密を使って考えると、簡単に答えを求めることができます。これを使って、｢先生は、パッと見ただけで、隠れている面の目の数の合計が分かるんですよ！｣と、マジックのように一瞬で答えを出し、みんなビックリ！！「さて、どうやったのでしょう？みんな考えてみて！」という流れでスムーズに進んでいく･･･予定だったのですが、その前の段階で予想以上に時間が掛かってしまったことで、フォロー役で入っていた私は内心ハラハラドキドキ。その後、少し予定を変更して先生が丁寧に説明を繰り返したことで、子ども達も理解でき、進行の流れが若干変わりはしたものの、何とか本時のまとめまでたどり着くことができました。
今回は難しい課題を扱う単元であり、その上授業参観で子ども達も緊張していたのか、なかなか思うように進まない部分もあったのですが、保護者の方が来てくれていた子ども達は、やはりとてもうれしそうでした。３年生になればかなりしっかりした子も多くなってきますが、そうはいってもまだ低学年ですから、自分が頑張っている姿をお父さん・お母さんに見てもらうことは何よりも励みになります。ついつい我が子には厳しい目を向けてしまいがちですが、授業参観のように子どもさんの頑張りを直接見ることができる機会には、ぜひとも温かい言葉をかけてあげてほしいと思います。子どもの側としても、お父さん・お母さんが見てくれているという思いは当然ありますから、励ましの言葉がもつ力はきっと普段の何倍にもなってお子さんの心に届くのではないでしょうか。
（butsuen）
