結晶性知能の発達に関する考察 その1
2014 年 11 月 3 日
先々週、先週と、算数・数学が入試で得点差の生じやすい教科であることを受け、その原因を考察してみました。
その際、知能には大きく分けて「流動性知能」と「結晶性知能」の2つがあるということをお伝えし、「流動性知能」に関わる単元がこの問題に深く関わることや、算数・数学の好き嫌いや得意不得意につながっているのではないか、ということをお伝えしました。そして、今からできる対策についても若干考えてみました。
この記事で、「流動性知能はどのようなものか」についてはかなり詳しくふれたと思います。しかし、いっぽうの「結晶性知能」についてはあまりふれませんでした。そこで、今回は「結晶性知能」の特徴についてお伝えしてみようと思います。
結晶性知能とは、言語、知識、思考、判断など、学習の積み重ねが生きる領域の知能で、「言語性知能」とも呼ばれています。この知能の呼称は、学習や体験によって得たものが結晶となって残り、より高いレベルの能力発揮に貢献することから名づけられたと言われます。
結晶性知能は、あらゆる教科の学力を支えています。何しろ、既有の知識を稼働させて考え、答えを導き出す知能なのですから。算数・数学においても、知識や理論、技能などに関わるものはみな結晶性知能の受けもつ領域です。では、この結晶性知能の発達曲線をもう一度見てみましょう。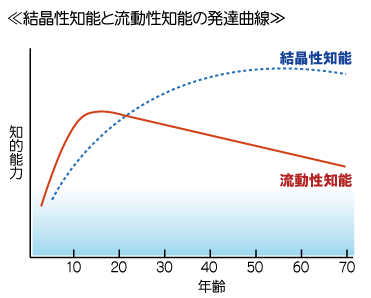
一見してわかるように、この知能は60歳頃になるまで伸び続けます。つまり、ほぼ一生伸ばし続けることができる知能なのです。このことは、子どもの学力形成に役立てるためにこのブログをお読みくださっている方々自身に対しても、大いに勇気を与えてくれるのではないでしょうか。
ただし、頭が柔らかい年齢期は暗記・記憶に強いため、ついそうした方向に学習が傾きがちです。それでテストの点を稼げる頭のよいお子さんも少なくありません。しかしながら、それをやると結晶性知能の特色である「学んで得たことが結晶となって積み重なり、より一層知能が高まる」といった好循環が生み出せなくなってしまいます。
もしも子どもがそうした方向に走ってしまうと、せっかくの才能も台無しになってしまいかねません。「学歴はあるけれど実力がない」という人間の話がよく取りざたされますが、そういったタイプの人間に陥る危険性が高いのです。
これと対照的な人物の話をご紹介しましょう。ノーベル物理学賞を受賞したアメリカの偉大な科学者、リチャード・ファインマン氏(1918-1988)の著作から引用したものです。
MIT(マサチューセッツ工科大学)時代、僕はいろいろないたずらをするのが好きだった。あるとき製図のクラスで、一人の学生が雲形定規(変てこな波形で、曲線を描くのに使うプラスチックの定規)を取り上げて、「この曲線に何か特別な公式でもあるかな?」と言った。僕はちょっと考えてから「むろんだよ。その曲線は特別な曲線なんだから。そらこの通り」と雲形定規をとりあげて、ゆっくり回し始めた。「雲形定規って奴は、どういう風に回しても、各曲線の最低点では接線が水平になるようにできているんだよ」
こうなるとクラスの連中が一人残らず自分の定規をいろいろな角度に持ち、この一番低い点に鉛筆をあてて回し始めた。みんなこの「発見」に沸き立ったが、誰もがとっくにかなり進んだところまで微積分をやっていて、「どんな曲線についても、極小点(最低点)での導関数(接線)はゼロ(つまり水平)である」ということは知り抜いているはずなのだ。ただそれを実際に当てはめてみることができなかっただけだ。言うなれば、自分の「知っている」ことすら知らなかったということになる。
これはいったいどうしたことなのだろう? 人は皆、物事を「本当に理解する」ことによって学ばず、たとえば丸暗記のようなほかの方法で学んでいるのだろうか? これでは知識など、すぐ吹っとんでしまうこわれ物みたいなものではないか。
単なる理系秀才で終わるか、優れた本物の科学者になるかの違いの根本を垣間見るような話ではないでしょうか。
ところで、中学受験においても、入試問題の大半はこの結晶性知能の守備範囲です。この知能をどうやって伸ばしたらよいのでしょうか。
今回も長くなってしまいましたので、この続きは次回以降に書いてみようと思います。
 このページは
このページは


